Excel VBA �m��

�������g��(�~���� Monte Carlo simulation)
�@����F
�@Rnd ���́A 0 �ȏ�A1 �����͈̔͂̒l�ŁA�������m���́A�P���x���������_���^ (Single) �̗�����Ԃ��܂��B��l�����ƌ����܂��B
�\��
Rnd[(number)]
���� number �͏ȗ��\�ł��B���� number �ɂ́A�P���x���������_���^ (Single) �̐��l�܂��͔C�ӂ̗L���Ȑ������w�肵�܂��B
| number �̒l | �߂�l |
| < 0 | ��ɁA���� number �̃V�[�h�l�ɂ���Č��܂铯�����l��Ԃ��܂��B |
| > 0 | �����n��̎��̗�����Ԃ��܂��B |
| = 0 | ���O�ɐ�������������Ԃ��܂��B |
| �ȗ������Ƃ� | �����n��̎��̗�����Ԃ��܂��B |
�@Randomize �X�e�[�g�����g�́A�����W�F�l���[�^�������� (�����n����Đݒ�) ���鐔�l���Z�X�e�[�g�����g�ł��B
�@Randomize �X�e�[�g�����g���g�p���Ȃ��ꍇ�A�������w�肵�Ȃ��� Rnd �����Ăяo���ƁA�ŏ��� Rnd �����Ăяo�����Ƃ��̃V�[�h�l�Ɠ����l���g�p����܂��B����ȍ~�́A���O�ɐ������ꂽ�����V�[�h�l�Ƃ��Ďg�p����܂��B
�@Randomize �X�e�[�g�����g���g�p����ƁA�V�X�e�� �^�C�}�[����擾�����l��V�����V�[�h�l�Ƃ��ė��������܂��B
�@HasTitle �v���p�e�B�́A�O���t�̃^�C�g���\���𐧌䂵�܂��BTrue �̏ꍇ�A����O���t�̃^�C�g����\�����܂��B�u�[���^ (Boolean) �̒l���g�p���܂��B
�w��͈͂̐��������������
�@�T�C�R���Ȃǂ�͕킷��Ƃ��ȂǂɎg������ł��B
�@���̃}�N�����_�E�����[�h�ł��܂��B��RandomValueCheckVBA01.xls
�@���s�� �� 10000 �Ƌψ�ȕ��z�ɂȂ�܂����A100 ����x���Ɛ���͈͂ł��傤���肪��������̂ł��ˁB
���K�����E�����E�w�������E�|�A�\��������
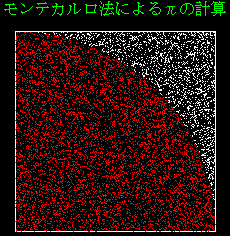
�@�����l�����̊����g���������ɁA���̗����̔������@���Љ�܂��B
�@���v���͂ł́A���̖ړI�Ƃ���m�����z�ɏ]���������g���ăV�~�����[�V�������܂��B
�@�����ł́A��\�I��4�̗���(���K�����E�����E�w�������E�|�A�\������)�������āA�q�X�g�O�����ŁA���̕��z�̌`���m�F���܂��B
�@�܂��AExcel�̊��Ōv�Z�����ݐϊm���ƁA���ʂ�Δ䂳���܂��B
�@�ȉ���VBA�R�[�h�́A��c�a������́uExcel VBA�ɂ�铝�v���v�f�[�^��͓����v�̃R�[�h���g�킹�Ă��������܂����B�v���O�����̗������������̉���́A���̏��Ђ����������߂ɂȂ邩�A�}���قȂǂʼn{�����ĉ������B
�@���̃}�N���ł́A�q�X�g�O������\�����邽�߂ɁAExcel�́u���̓c�[��-VBA�v���g���Ă��܂��B�u���̓c�[��-VBA�v�́AExcel�œ��v��Z�p�v�Z�Ɋ�Â����͂����s���邽�߂́A�A�h�C���@�\�ł��B
�@[�c�[��] ���j���[�� [���̓c�[��-VBA] ���\������Ȃ��ꍇ�́A[�c�[��] ���j���[��[�A�h�C��]�ŕ\������郊�X�g�{�b�N�X�� [���̓c�[��-VBA] �Ƀ`�F�b�N�����āA�v���O�������C���X�g�[�����ĉ������B
�@Vista �̏ꍇ�́A�u�t�@�C���v���uExcel�̃I�v�V�����v�ŕ\�������A���̉�ʂŁA�u�ݒ�v�{�^���������܂��B
�@����ƁA���X�g�{�b�N�X���\������܂��B
�@���̃}�N���ł́AExcel�̃o�[�W�������擾���āA[���̓c�[��-VBA] �̊g���q���A�����ŕύX����悤�ɂ��Ă��܂��B
�@Excel2003 �ȑO�́AATPVBAEN.XLA!Histogram ���������̂��A
Excel2007�`�́AATPVBAEN.XLAM!Histogram �ƁA4���g���q�ɕύX���Ă��邩��ł��B
�@Microsoft �Ђ́A�Ȃ�����ȂƂ����ύX����I�@�����{��I�I
�@���̃}�N�����_�E�����[�h�ł��܂��B��RandomNumbersVBA4.xls
�@(���́u���������v�́A[���̓c�[��-VBA] ���g���Ă��邽�߂��A�u���E�U�̉�ʂŊJ������Ԃł͎��s�ł��܂���B��������_�E�����[�h���āAExcel �ŊJ���āA���s���ĉ������B
�@�g�����́A�����ꂩ�́u�����v�̃{�^�������������ł��B���x�ł��A�����܂��B)
�@�}�N���̗��p���@�̗�F
�@���������10��U���āA1�̏o��́H
���@�����ŁA�m����1/6�A��10�Ƃ��Ď��s���܂��B
�A�������5�ʂ̃��C��������l���A�S�����C�������Ȃ����́A���̓������H
���C����10�ʈȏ�����͉����H
���@�|�A�\�������ŁA���ϓ�������5�Ŏ��s���܂��B
�@���@�R�����@��
�@�Ԃō������H�𑖂��Ă��āA�C���^�[�`�F���W�ł̎Ԃ̏o���肪�����̂ɁA����̓r����A�g���l���̓������O�ŁA�a���āA�~�܂肻���ɂȂ邱�Ƃ�����܂��ˁB
�@���̂����A���炭�s���ƁA�ςɂ܂܂ꂽ�悤�ɁA�a���������āA�Ԋԋ������āA�����ő����悤�ɂȂ�܂��B
�@����́A�҂��s��ł͂Ȃ��A�P�ʎ��Ԃ�����̏����\�̖͂��ł��B
�@������b���ɒ����Ĕ�r���Ă݂܂��傤�B
�@����(100km)���b��(28m)
�@����(�@4km)���b��( 1m)
�@����100km�ő����Ă���Ƃ��́A1�b�Ԃ�28m����܂����A�����Ă��邭�炢�ɒx���Ȃ�ƁA1�b�Ԃ�1m��������܂���B
�@�Ԃ̒����� 5m �Ƃ���ƁA�X�s�[�h���x���Ȃ�ƁA�b�� 1m x 5 = 5m �ŁA�Ԃ�����Ȃ���ԂɂȂ��Ă��܂���ʗʂł��A����100km���� �b�� 28m x 5 = 135m �ŁA�[���ȎԊԋ����������đ����̂ł��B
�@���̎������猾���邱�Ƃ́A�������H�̓r���ŏa���Ă���Ƃ��ɂ́A�a�̌���
�u���̐�a�ؒ��I���x���Ƃ��I�v
�Ƃ����f�����o���̂͋t���ʂŁA�a�̗ǂ�ǂ��Ȃ��Ă��܂��\��������܂��B
�@�ނ���A�a�̐擪�����ɁA
�u�㑱�Ԃ��a���Ă��܂��B�����ƃX�s�[�h���グ�đ���܂��傤�I�v
�Ƃ����x����\�����ׂ��Ȃ̂ł��B
(^^)/~~~
|
�@���v�f�[�^��͂̏ڂ������@�ɂ��ẮA���L�̃T�C�g���A�����������B
(^^�U
�usda-trial.xls�v�̃V�[�g�u�X���b�g�}�V���v�́u�����̊ȒP�ȉ��p��v�́A���߂��Ȃ��悤�ɁI
�@�|�A�\����������2���W���[���́A���̃T�C�g�̃R�[�h���g�킹�Ă��������܂����B
�@�܂��A�u�҂��s��̃V�~�����[�V�����v�̃R�[�h���x�[�X�ɁA�A�j���[�V�������ɃA�����W�������̂��ARandomNumbersVBA4.xls �̃V�[�g�u�҂��s��v�ɁA���܂��ɕt���܂����B
(�u�҂��s��v�́A�u���E�U�ŊJ������Ԃł��Asimulate �{�^���������ƁA�����܂��B)
�NjL�F Excel �́u�R���g���[���c�[���{�b�N�X�v�́u�R�}���h�{�^���v�Ƀ}�N����o�^�����Ƃ��A�}�E�X�|�C���^���{�^���ɏd�˂Ă��A�|�C���^�̌`�͖��̂܂܂ŁA��(�w)�̌`�ɂ͂Ȃ�܂���B
�@�����ł́A���̃T�C�g���Q�l�ɂ����Ă��������AMouseMove�C�x���g�ŁA��̌`�ɂȂ�悤�ɂ��܂����B
�@(�X�ɒ��ׂ��Ƃ���A�u�t�H�[���v�́u�{�^���v���g���ƁA����Ŏ�̌`�ɂȂ邱�Ƃ�����܂����B)
�@�֘A�ł����A���y�̐��E�ł́A�s���N�m�C�Y�ƌĂ����g�����z�́u����(�m�C�Y)�v���g���܂��B
�@�m�C�Y�ɂ́A��������g����������l�Ɋ܂ރz���C�g�m�C�Y(���F�G�� white noise 1Hz���Ƃ̉��̃G�l���M�[��������)�ƁA���g���ɔ���Ⴕ�āA�������g���̉��قǎキ�Ȃ�s���N�m�C�Y(pink noise �܂��͂P�^���G�� �P�I�N�^�[�u���Ƃ̃G�l���M�[��������)���L��܂��B
�@���ɗႦ��ƁA���ׂĂ̔g���̌����܂ތ������F���ŁA���g�����Ⴂ�i�g���������j�����́A�Ԃ����Ȃ̂ŁA�Ⴂ���g���̃��x�����傫����A���F���Ԃ݂������Ă���Ƃ������ƂŃs���N�ƕ\���������̂ł��B
�@�z���C�g�m�C�Y�̗�́A�e���r�̕����I����́A��ʂ��u�����v��Ԃ̂Ƃ��̉���AFM�����̋NJԃm�C�Y�ŁA�u�V���[�c�v�ƕ���������̂ł��B�@�B�I�ɔ��������₷���m�C�Y�ł��B
�@�l�Ԃ̎��́A���g���ɑ���(���ʂɑ��Ă�)�ΐ��I�Ɋ�����悤�ɂł��Ă��܂��B�����̃I�N�^�[�u�̈Ⴂ�́A�l�Ԃ̎��ɂ͓��Ԋu�ɕ������܂����A���g���ŃI�N�^�[�u�̈Ⴂ�́A���g���̔䗦��2�{�ɂȂ��Ă��܂��B(100Hz��200Hz��400Hz��800Hz�E�E)
�@�s���N�m�C�Y�́A���̐l�Ԃ̎��̓�������ɍl����ꂽ���̂ŁA������̓z���C�g�m�C�Y�����ቹ�悪�����Ă���̂ŁA�u�U�[�c�v�ƕ������܂��B�������i�̎��g�������̕]���ɂ́A���̃s���N�m�C�Y���g���܂��B�z���C�g�m�C�Y���A-3dB/oct �̒��ʉ߃t�B���^�iLow Pass Filter�j�ɒʂ��č��o���܂��B(�s���N�m�C�Y�E�W�F�l���[�^)
�@����F
�@Function �X�e�[�g�����g�́AFunction �v���V�[�W���̖��O�A�����A����і{�̕������\������R�[�h��錾���܂��B
�\��
[Public | Private | Friend] [Static]
Function name [(
arglist)] [As type]
[statements]
[name = expression]
[Exit Function]
[statements]
[name = expression]
End Function
�@
name �K���w�肵�܂��B��`���� Function �v���V�[�W���̖��O���w�肵�܂��B�ϐ��̕W���I�Ȗ��O�t���K���ɏ]���Ďw�肵�܂��B
�@����
arglist �́A���̌`���Ŏw�肵�܂��B
[Optional] [
ByVal | ByRef] [ParamArray] varname[( )] [As type] [= defaultvalue]
�@�����̒l�n��
ByVal �ƁA�Q�Ɠn��
ByRef �̈Ⴂ
http://shuhho.hatenablog.com/entry/excelvba-37 http://officetanaka.net/excel/vba/tips/tips94.htm
http://msdn2.microsoft.com/ja-jp/library/eek064h4(VS.80).aspx
http://officetanaka.net/excel/vba/tips/tips94.htm
http://msdn2.microsoft.com/ja-jp/library/eek064h4(VS.80).aspx
�@
ByRef �F�Q�Ɠn��
�@���ׂĂ̈����́A���Ɏw�肵�Ȃ�����A�Q�Ɠn����Function �v���V�[�W���ASub �v���V�[�W���Ɉ����n����܂��B
�@�f�t�H���g�̓n�����ł��B
�@�Q�Ɠn�����g���ƁA�Ăяo�����̃R�[�h�ɂ���A��̃v���O���~���O�v�f���A�v���V�[�W�����璼�ڎQ�Ƃł���悤�ɂ��܂��B
�@Sub �ň�����n���Ƃ��́A�߂�l���ق������߂Ȃ̂ŁA�Q�Ɠn��(���w��̂܂�)���g���ꍇ�������ł��傤�B
�@���C����������ACall ���� Sub �̃v���V�[�W���ɓn�����ϐ����ASub �ʼn��H���Ă�����āA���C���ɖ߂��Ă��炤�ꍇ���A�Q�Ɠn���ł��B
�@�Q�Ɠn���́A�����̃f�[�^�^�ɊW�Ȃ��A���ׂĂ̈������n�����Ƃ��̏��v���Ԃ���уv���V�[�W�����̃������̈� (4 �o�C�g) �������ł��邽�߁A�����I�ł��B
�@
ByVal �F�l�n��
�@�l�n�� (�l�ɂ������n��) ���g�p����ƁA���̕ϐ�(��ɂȂ�v���O���~���O�v�f)�̒l���A�v���V�[�W�����̃��[�J���ϐ��ɃR�s�[���܂��B
�@�v���V�[�W�� �R�[�h����Ăяo�����̃R�[�h�ɂ���A��̗v�f�ɃA�N�Z�X���邱�Ƃ͂���܂���B
�@���������āA�Ăяo���ꂽ�v���V�[�W�����œn���ꂽ�ϐ��̒l��ύX���Ă��A�Ăяo�����̃v���V�[�W�����Q�Ƃ��錳�̕ϐ��̒l�͕ύX����܂���B
�@�l�œn���������́A�����̃f�[�^�^�ɉ����āA�v���V�[�W������ 2 �` 16 �o�C�g�̃������̈���g�p���܂��B
�@�f�[�^�^���傫���قǁA�l�n���ɗv���鎞�Ԃ����������Ȃ�܂��B
�@������l�n���œn���ɂ́A�v���V�[�W����`���őΉ�����p�����[�^�� ByVal �L�[���[�h���w�肵�܂��B
�@Function �̃f�t�H���g�́A�u�Q�Ɠn���v�ł��B
�@������^�ϐ��́A�f�[�^�ʂ������Ȃ�̂ŁA
Function ���Ŗ߂�l��ύX���Ȃ����Ƃ����炩�ȕ�����^�ϐ��͏ꍇ�Ɍ����ẮA�f�t�H���g�́u�Q�Ɠn���v�̂܂܂ŗǂ��ł��B���̂ق����A�����������Ȃ��A�������x�������Ȃ�܂��B
�@�������A������ Function ���ŕύX����ꍇ�́A
ByVal ���I�Ɏw�肵�āA���C�������ƕ��������K�v������܂��B
�@ByVal (�l�n��) ���邱�ƂŁA���C�������̕ϐ��̒l���AFunction ���ŕς����Ă��A���C�������ɉe����^���邱�Ƃ͂Ȃ��Ȃ�܂��B
�@�t�Ɍ����A�f�t�H���g�́u�Q�Ɠn���v���g���ꍇ�́A
Function ���ň����̒l��ς��Ȃ��H�v ���K�v�ł��B
�@Application �v���p�e�B�́A�I�u�W�F�N�g��Ԃ��v���p�e�B�ł��B
�@�ΏۂƂȂ�I�u�W�F�N�g���w�肳��Ȃ��ꍇ�́AExcel �A�v���[�V���� (Application �I�u�W�F�N�g) ��Ԃ��܂��B
�@�ΏۂƂȂ�I�u�W�F�N�g���w�肳�ꂽ�ꍇ�́A�w�肳�ꂽ�I�u�W�F�N�g���쐬���� Application �I�u�W�F�N�g��Ԃ��܂��BOLE �I�[�g���[�V�������g���Ă��āA�I�u�W�F�N�g�̃A�v���P�[�V�����ɃA�N�Z�X����Ƃ��ȂǂɁA���̃v���p�e�B���g���܂��B�l�̎擾�̂݉\�ł��B
�@NormSInv �́AExcel �̊��ŁA�W�����K���z�̗ݐϕ��z���̋t���̒l��Ԃ��܂��B
�@���̕��z�́A���ς� 0 �ŕW������ 1 �ł��鐳�K���z�ɑΉ����܂��B
�@NormSInv(�m��)
�@�m���@���K���z�ɂ�����m�����w�肵�܂��B
���ӁF
�@�m���ɐ��l�ȊO�̒l���w�肷��ƁA�G���[�l #VALUE! ���Ԃ���܂��B
�@�m�� < 0�A�܂��͊m�� > 1 �ł���ꍇ�A�G���[�l #NUM! ���Ԃ���܂��B
�@�m���̒l���w�肳���ƁANORMSDIST(z) = �m���ƂȂ�悤�Ȓl z ���V�[�N����܂��B���������āANORMSINV ���̐��x�� NORMSDIST ���̐��x�Ɉˑ����܂��BNORMSINV ���ł́A�����v�Z�̎�@�����p����܂��B100 ���v�Z���J��Ԃ��Ă��v�Z���ʂ��������Ȃ��ꍇ�A�G���[�l #N/A ���Ԃ���܂��B
�@NormDist �́A�w�肵�����ςƕW�����ɑ��鐳�K���z���̒l��Ԃ��܂��B
�@���̊��́A����������n�߂Ƃ��铝�v�w�̕��L������ɉ��p�ł��܂��B
�@NormDist(x,����,�W����,���`��)
�@x�@���ɑ������l���w�肵�܂��B
�@�����@�ΏۂƂȂ镪�z�̎Z�p���� (��������) ���w�肵�܂��B
�@�W�����@�ΏۂƂȂ镪�z�̕W�������w�肵�܂��B
�@���`���@�v�Z�Ɏg�p����w�����̌`����_���l�Ŏw�肵�܂��B���`���� TRUE ���w�肷��Ɨݐϕ��z���̒l���v�Z����AFALSE ���w�肷��Ɗm�����x���̒l���v�Z����܂��B
���ӁF
�@���ρA�W�����ɐ��l�ȊO�̒l���w�肷��ƁA�G���[�l #VALUE! ���Ԃ���܂��B
�@�W���� <= 0 �ł���ꍇ�A�G���[�l #NUM! ���Ԃ���܂��B
�@���� = 0 �A�W���� = 1 �����`�� = TRUE �ł���ꍇ�A�W�����K���z�� (NORMSDIST ��) �̒l���v�Z����܂��B
�@NormSDist �́A�W�����K���z�̗ݐϕ��z���̒l��Ԃ��܂��B
�@���̕��z�́A���ς� 0 (�[��) �ŕW������ 1 �ł��鐳�K���z�ɑΉ����܂��B���K���z�\�̑���ɂ��̊����g�p���邱�Ƃ��ł��܂��B
�@BinomDist �́A���z�̊m�����̒l��Ԃ��܂��B
�@���̊��́A���̎��s�����̒��ŁA���s�̌��ʂ������܂��͎��s�̂����ꂩ�ł���ꍇ�A���s���Ɨ��������̂ł���ꍇ�A��������ʂ��Đ����̊m�������ł���ꍇ�Ɏg�p���܂��B
�@���Ƃ��A���ɐ��܂�� 3 �l�̐Ԃ����̒��� 2 �l���j�̎q�ł���m�����v�Z���邱�Ƃ��ł��܂��B
�@BinomDist(������,���s��,������,���`��)
�@�������@���s�Ɋ܂܂�鐬���̉��w�肵�܂��B
�@���s���@�Ɨ����s�̉��w�肵�܂��B
�@�������@1 ��̎��s����������m�����w�肵�܂��B
�@���`���@���̌`�����A�_���l�Ŏw�肵�܂��B���`���� TRUE ���w�肵���ꍇ�ABINOMDIST ���̖߂�l�͗ݐϕ��z���ƂȂ�A0 �` ��������͈̔͂Ő�����������m�����v�Z����܂��BFALSE �̏ꍇ�́A�m�����x���ƂȂ�A���m�ɐ�������̐�����������m�����v�Z����܂��B
�@���ӁF
�@�������A���s�ɐ����ȊO�̒l���w�肷��ƁA�����_�ȉ�����̂Ă��܂��B
�@�������A���s�A�������ɐ��l�ȊO�̒l���w�肷��ƁA�G���[�l #VALUE! ���Ԃ���܂��B
�@������ < 0 �܂��͐����� > ���s�̏ꍇ�A�G���[�l #NUM! ���Ԃ���܂�
�@������ < 0 �܂��͐����� > 1 �̏ꍇ�A�G���[�l #NUM! ���Ԃ���܂��B
�@RoundUp ���́A���l���w�肳�ꂽ�����ɐ�グ��Excel�̊��ł��B
�@WorksheetFunction �v���p�e�B��O�ɕt����K�v���L��܂��B
�@RoundUp(���l,����)
���l�@��グ�̑ΏۂƂȂ�����l���w�肵�܂��B
�����@���l���̂Ă����ʂ̌������w�肵�܂��B
�@ROUNDUP ���́AROUND ��(�l�̌ܓ�)�Ɏ������������܂����A��ɐ��l�̐�グ���s���_���قȂ�܂��B
�����ɐ��̐����w�肷��ƁA���l�͏����_�̉E (�����_�ȉ�) �̎w�肵�����ɐ�グ���܂��B
������ 0 ���w�肷��ƁA���l�͍ł��߂������ɐ�グ���܂��B
�����ɕ��̐����w�肷��ƁA���l�͏����_�̍� (��������) �̎w�肵���� (1 �̈ʂ� 0 �Ƃ���) �ɐ�グ���܂��B
�@Round ���́A�w�肳�ꂽ�����_�ʒu�Ŏl�̌ܓ��������l��Ԃ��܂��B
�@Round(expression [,numdecimalplaces])
expression�@�K���w�肵�܂��B�l�̌ܓ����s���������w�肵�܂��B
numdecimalplaces�@�ȗ��\�ł��B�l�̌ܓ����s�������_�ȉ��̌�����\�����l���w�肵�܂��B�ȗ�����ƁARound ���͐����l��Ԃ��܂��B
�@Excel��Round ���́A���̌����ɕ��̐����w�肷��ƁA���l�͏����_�̍��� (��������) �̎w�肵���� (1 �̈ʂ� 0 �Ƃ���) �Ɏl�̌ܓ�����܂��B�������AVBA�̊��ł́A�����͎g���܂���B
��: Round(2.149, 2) �Ƃ���ƁA2.149 �������_��2�ʂɎl�̌ܓ����܂� (2.15)
�@Int(number) ���� Fix(number) ���́A�ǂ�������� number �̏�����������菜��������������Ԃ��܂��B
�@����
number �ɕ��̒l���w�肵���ꍇ�ɂ́A
Int ��������
number ���Ȃ��ő�̕��̐�����Ԃ��̂ɑ��āA
Fix ���͈���
number �ȏ�̍ŏ��̕��̐�����Ԃ��܂��B
�@���Ƃ��A�����Ƃ��� -8.4 ���w�肷��ƁAInt ���� -9�AFix ���� -8 �����ꂼ��Ԃ��܂��B
�@Fix(
number) �́A���̐����Ɠ����ł��B
Sgn(
number) * Int(
Abs(
number))
�@ExponDist ���́A�w�����z����Ԃ��܂��B
�@���̊��́A��s�� ATM �Ō����������o���̂ɂ����鎞�ԂȂǁA�C�x���g�̊Ԋu�����f��������ꍇ�Ɏg�p���܂��B
�@���Ƃ��A���鏈���� 1 ���ȓ��ɏI������m�����Z�o���邱�Ƃ��ł��܂��B
�@ExponDist(x,��,���`��)
x�@���ɑ������l���w�肵�܂��B
���@�p�����[�^�̒l���w�肵�܂��B
���`���@�v�Z�Ɏg�p����w�����̌`����_���l�Ŏw�肵�܂��B���`���� TRUE �̏ꍇ�A�߂�l�͗ݐϕ��z���ƂȂ�AFALSE �̏ꍇ�́A�m�����x�����Ԃ���܂��B
�@���ӁF
x �܂������ɐ��l�ȊO�̒l���w�肷��ƁA�G���[�l #VALUE! ���Ԃ���܂��B
x <0 (���̐�) ���w�肷��ƁA�G���[�l #NUM! ���Ԃ���܂��B
�� <=0 �ł���ꍇ�A�G���[�l #NUM! ���Ԃ���܂��B
�@Poisson ���́A�|�A�\���m���̒l��Ԃ��܂��B
�@�ʏ�A�|�A�\�����z�͈��̎��ԓ��ɋN���鎖�ۂ̐���\�����邽�߂ɗ��p����܂��B
�@���Ƃ��A�������H�̗������� 1 ���Ԃɒʉ߂��鎩���Ԃ̑䐔��\�����邱�Ƃ��ł��܂��B
�@Poisson(�C�x���g��,����,���`��)
�C�x���g���@�����鎖�ۂ̐����w�肵�܂��B
�����@���̎��ԓ��ɋN���鎖�ۂ̕��ϒl���w�肵�܂��B
���`���@�m�����z���v�Z������`�����A�_���l�Ŏw�肵�܂��B���`���� TRUE ���w�肵���ꍇ�A���N���郉���_���Ȏ��ۂ̐��� 0 �����C�x���g���͈̔͂ł���悤�ȗݐσ|�A�\���m�����v�Z����܂��BFALSE �̏ꍇ�́A���N���鎖�ۂ̐������m���C�x���g���ƂȂ�悤�ȃ|�A�\���m�����v�Z����܂��B
�@���ӁF
�@�C�x���g���ɐ����ȊO�̒l���w�肷��ƁA�����_�ȉ�����̂Ă��܂��B
�@�C�x���g���A�����ɐ��l�ȊO�̒l���w�肷��ƁA�G���[�l #VALUE! ���Ԃ���܂��B
�@x < 0 �̏ꍇ�A�G���[�l #NUM! ���Ԃ���܂��B
�@���� <= 0 �̏ꍇ�A�G���[�l #NUM! ���Ԃ���܂��B
�@IIf ���́A���̕]�����ʂɂ���āA2 �̈����̂��� 1 ��Ԃ��܂��B
�@
IIf(
expr, truepart, falsepart)
�@IIf ���̍\���́A���̖��O�t����������\������܂��B
| �w�荀�� | ���e |
|
expr | �K���w�肵�܂��B�]���Ώۂ̎����w�肵�܂��B |
|
truepart | �K���w�肵�܂��B���O�t������ expr ���^ (True) �̏ꍇ�ɕԂ��l�܂��͎����w�肵�܂��B |
|
falsepart | �K���w�肵�܂��B���O�t������ expr ���U (False) �̏ꍇ�ɕԂ��l�܂��͎����w�肵�܂��B |
�@���ӁF
�@IIf ���ł́A���O�t������ truepart �܂��͖��O�t������ falsepart �̂����ꂩ����������Ԃ���܂����A�]���͗����̈����ɑ��čs���܂��B
�@���̂��߁AIIf �����g���ƁA�\�����Ȃ����ʂ��N���邱�Ƃ�����܂��B���Ƃ��A���O�t������ falsepart ��]���������� 0 �ɂ�鏜�Z�G���[����������ꍇ�́A���O�t������ expr ���^ (True) �ł����Ă��G���[���������܂��B
�@���O�t�������Ƃ́A�I�u�W�F�N�g ���C�u�����ɂ��炩���ߒ�`���ꂽ���O���������ł��B
�@���O�t���������g�p����ƁA�\���ǂ���Ɏw�肳�ꂽ�����Ŋe�����ɒl���w�肵�Ȃ��Ă��A�C�ӂ̏����Œl��ݒ肷�邱�Ƃ��ł��܂��B
�@���Ƃ��A3 �̈������擾�ł��鎟�̂悤�ȃ��\�b�h������Ƃ��܂��B
DoSomeThing namedarg1, namedarg2, namedarg3
�@���O�t���������g���ƁA���̂悤�Ɉ������w�肷�邱�Ƃ��ł��܂��B
DoSomeThing namedarg3 := 4, namedarg2 := 5, namedarg1 := 20
�@���O�t�������́A�\���̕W���I�Ȕz�u�����Ŏw�肷��K�v�͂���܂���B
���̈Öْm�\�͌���v�����g
�@�e���r�E�h���}�u�h���S�����v�ŏЉ��Ă����v�Z�h����������}�N��������Ă݂܂����B
�@�o�ꂷ�鐔�l�͈̔͂�ς��āA��Փx���ł��܂��B
�E�Z�� ���w�A�����ł��邩�ǂ����͏��Q�Z���Ō��܂�
�E���̈Öْm��g�ɂ��邽�߂ɂ̓X�p���^�����ʓI
�E���̈Öْm��g�ɂ�����@�@�u���� ���̈Öْm�\�͌���v�����g�v
�@���̃}�N�����_�E�����[�h�ł��܂��B�� MathWorkbookVBA04.xls